By

文章目录
  1. 1. 二叉树定义
  2. 2. 前序遍历
  3. 3. 中序遍历
  4. 4. 后序遍历

二叉树是一种非常常见的数据存储结构，在数值查找、排序、遍历访问等方面都有应用。根据树的特点，用于数值查找和排序的二叉树有最大堆和最小堆，这是一类特殊的二叉树。对一般的二叉树而言，所能做的通用操作就是遍历。我在这里详细介绍一下二叉树的遍历。

二叉树定义

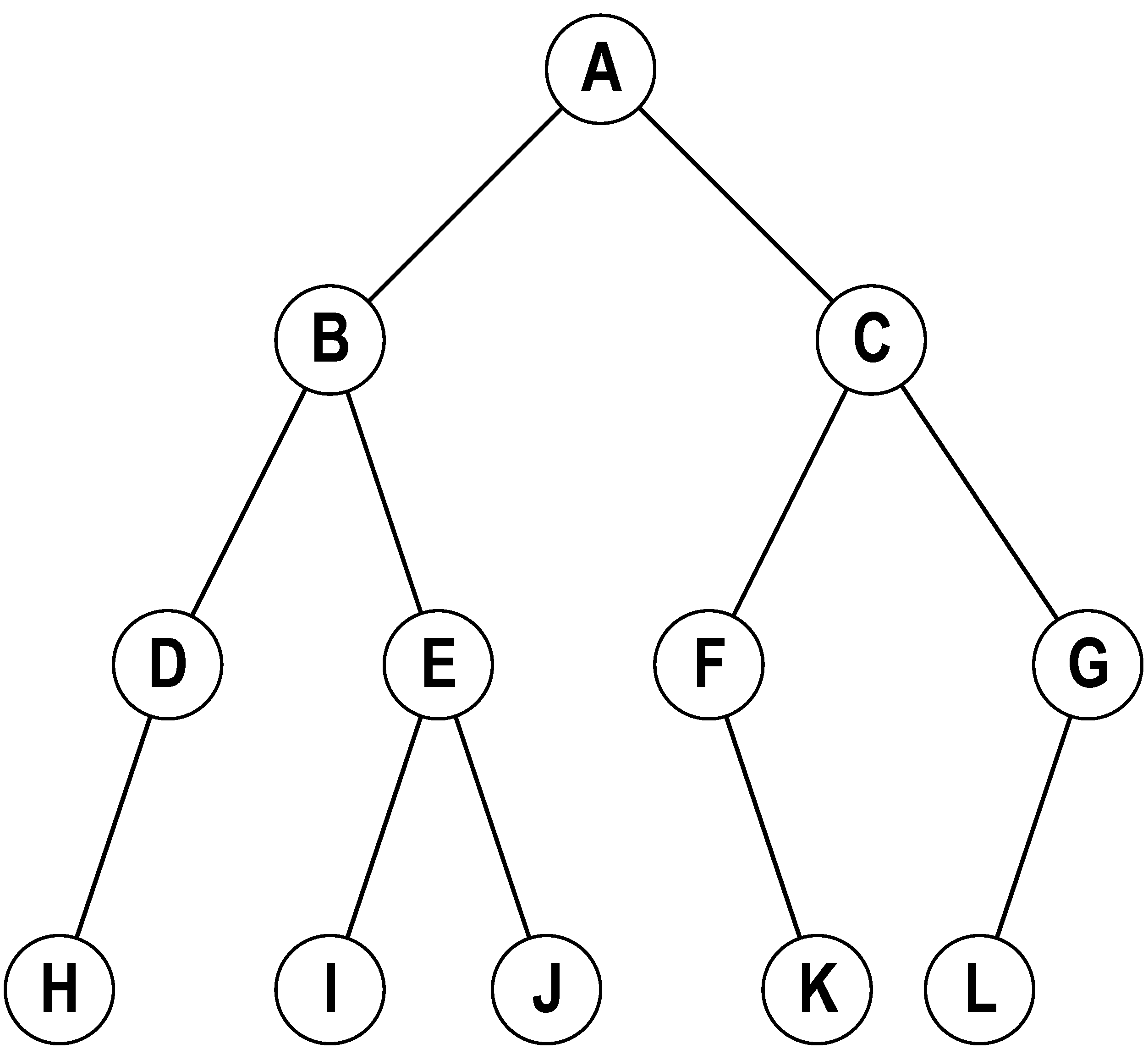
二叉树，顾名思义，有一个根节点处于树的顶层，且树中每个节点有至多两个子节点。一般，我们称一个节点的左子节点为左孩子，右子节点为右孩子。如下图，一个包含12个节点的二叉树。

图-1. 二叉树


采用Java定义二叉树的节点

1
2
3
4
5
class Node {
    String value;
    Node left = null;
    Node right = null;
}

left和right分别是当前节点的左孩子和右孩子。若要遍历如图-1的二叉树，根据节点的访问顺序，主要有三种方式：前序遍历、中序遍历和后序遍历。三种遍历方式的节点访问顺序为：

  • 前序遍历： 父节点，左子树，右子树；
  • 中序遍历： 左子树，父节点，右子树；
  • 后序遍历： 左子树，右子树，父节点；

下面将详细解说这三种遍历方式。

前序遍历

前序遍历的访问顺序是：父节点，左孩子，右孩子。

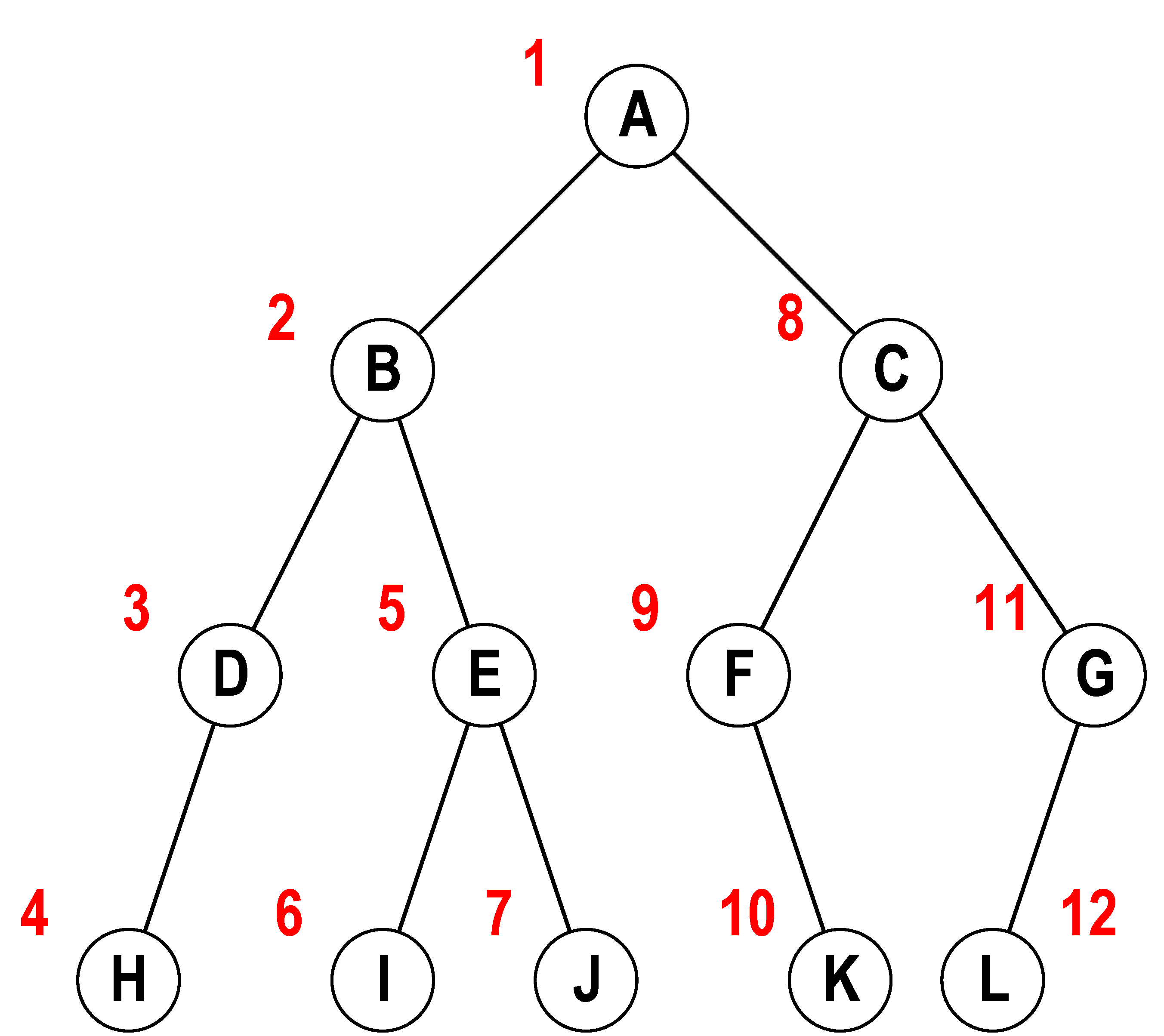
图-2. 前序遍历二叉树


图-2中的数字代表前序遍历时节点的访问次序。
采用递归方式进行前序遍历相对比较简单：先访问根节点，然后递归地遍历左子树，再递归地遍历右子树。
前序遍历（递归）的Java代码如下

1
2
3
4
5
6
7
8
9
void PreOrderTraversal(Node T) {
    if(T == null) {
    	return;
    }
    System.out.println(T.value);    // 访问根节点
    PreOrderTraversal(T.left);      // 遍历左子树
    PreOrderTraversal(T.right);     // 遍历右子树
    return;
}

有些情况下，需要非递归地实现二叉树的遍历。前序遍历的非递归思路是：

  1. 访问根节点，将根节点入栈；
  2. 若栈顶节点存在左孩子，则访问左孩子并将其入栈；若不存在左孩子，弹出栈顶节点，访问右孩子并将其入栈

前序遍历（非递归）的Java代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
void PreOrderTraversalNonRecursive(Node T) {
    List<Node> stack = new ArrayList<>();
    Node pT = T;
    while(pT != null || !stack.isEmpty()) {
        if(pT != null) {
            System.out.println(pT.value);
            stack.add(pT);
            pT = pT.left;
        } else {
            pT = stack.remove(stack.size() - 1).right;
        }
    }
}

中序遍历

中序遍历的访问顺序是：左孩子，父节点，右孩子。

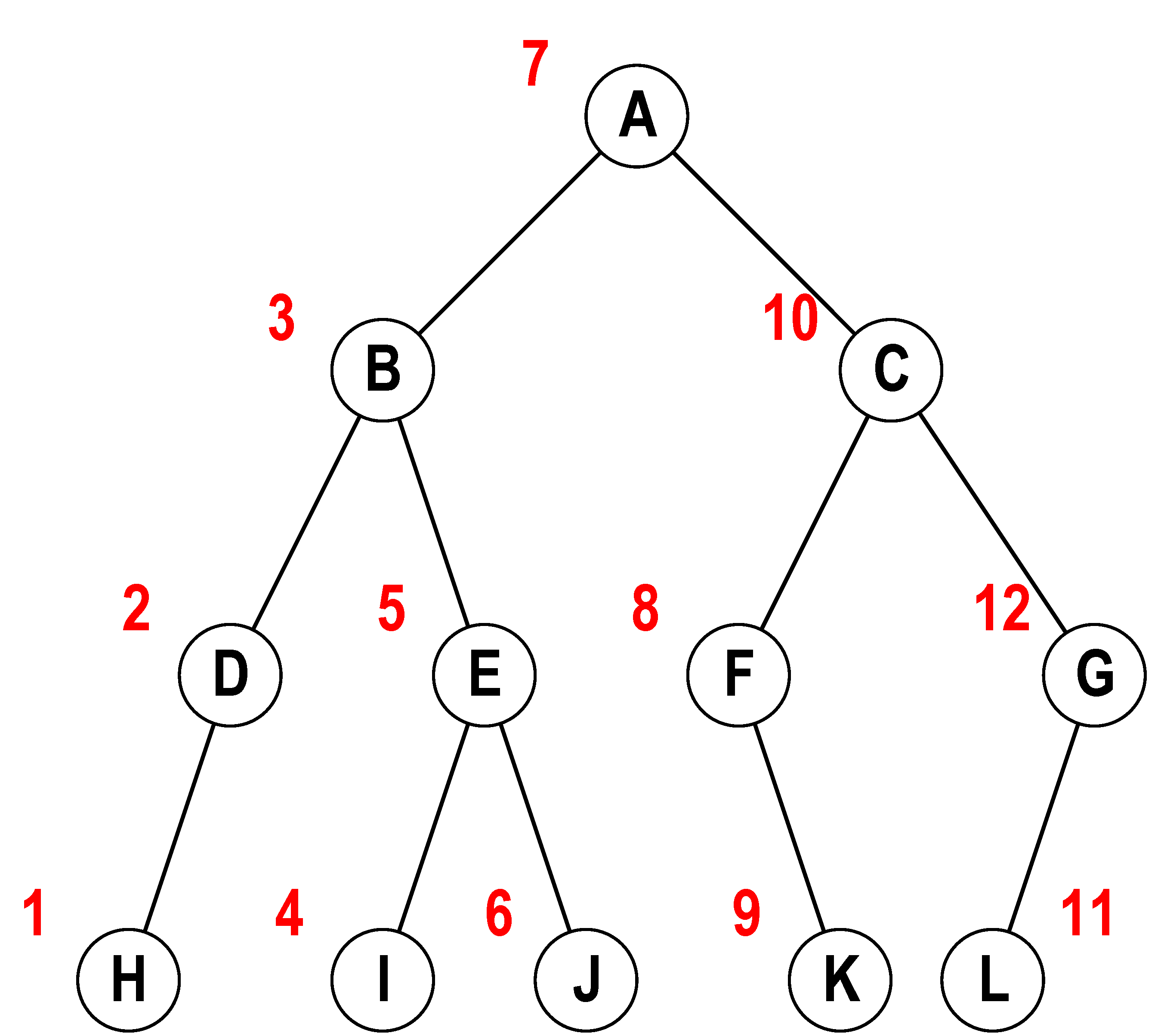
图-3. 中序遍历二叉树


图-3中的数字代表中序遍历时节点的访问次序。
采用递归方式进行中序遍历相对比较简单：先递归地遍历左子树，然后访问根节点，再递归地遍历右子树。
中序遍历（递归）的Java代码如下

1
2
3
4
5
6
7
8
9
void InOrderTraversal(Node T) {
    if(T == null) {
    	return;
    }
    InOrderTraversal(T.left);
    System.out.println(T.value);
    InOrderTraversal(T.right);
    return;
}

非递归中序遍历的思路是：

  1. 将根节点入栈；
  2. 循环地将栈顶节点的左孩子入栈，直到栈顶节点不存在左孩子；
  3. 访问栈顶节点并出栈。若其存在右孩子，则将右孩子入栈，重复步骤2；否则，重复步骤3；

中序遍历（非递归）的Java代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void InOrderTraversalNonRecursive(Node T) {
    List<Node> stack = new ArrayList<>();
    Node pT = T;
    while(pT != null || !stack.isEmpty()) {
        if(pT != null) {
            stack.add(pT);
            pT = pT.left;
        } else {
            pT = stack.remove(stack.size() - 1);
            System.out.println(pT.value);
            pT = pT.right;
        }
    }
}

后序遍历

后序遍历的访问顺序是：左孩子，右孩子，父节点。

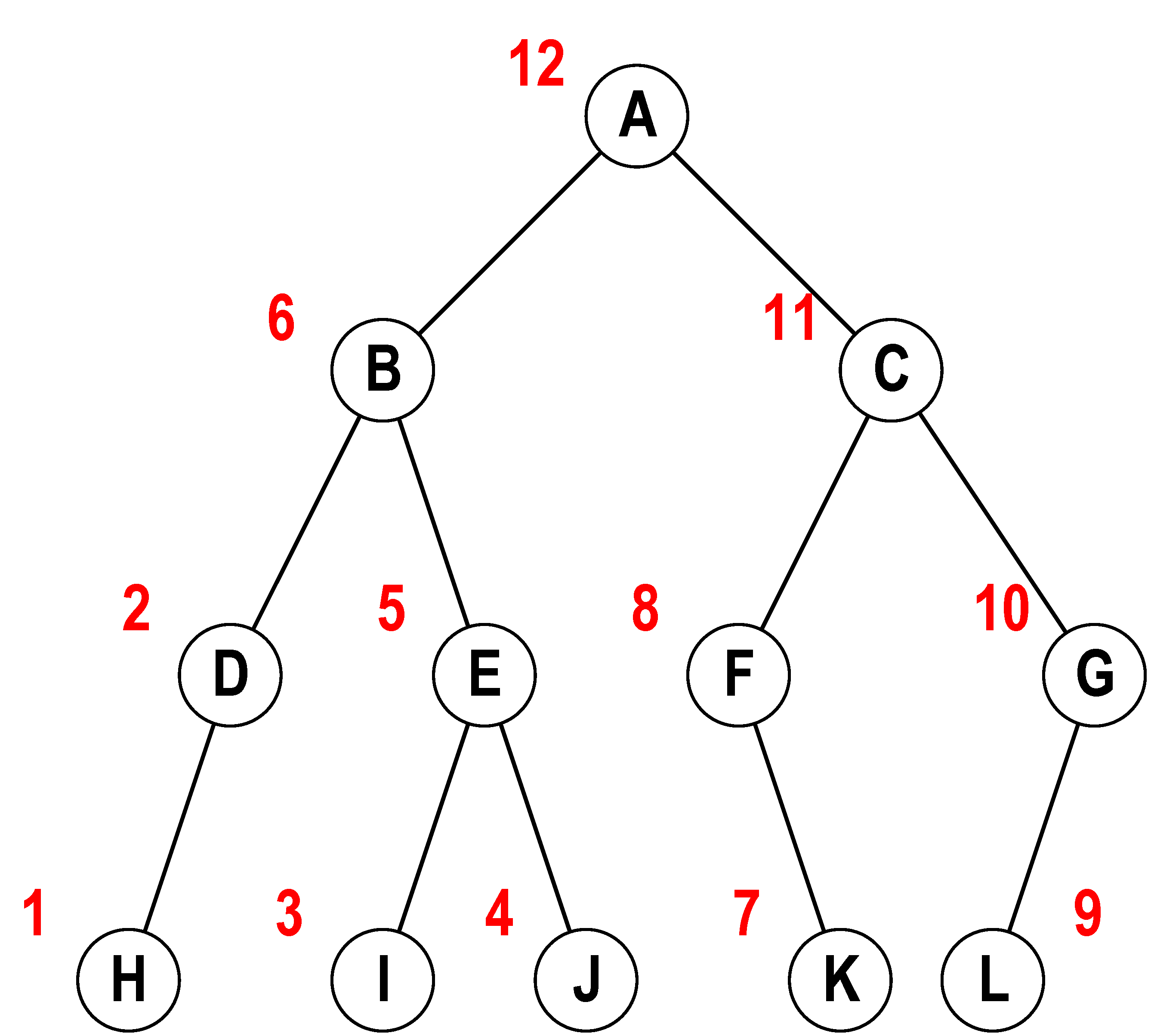
图-3. 后序遍历二叉树


图-3中的数字代表后序遍历时节点的访问次序。
采用递归方式进行后序遍历相对比较简单：先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。
后序遍历（递归）的Java代码如下

1
2
3
4
5
6
7
8
9
void PostOrderTraversal(Node T) {
    if(T == null) {
    	return;
    }
    PostOrderTraversal(T.left);
    PostOrderTraversal(T.right);
    System.out.println(T.value);
    return;
}

非递归后序遍历的思路是：

  1. 将根节点入栈，最近访问的节点为preT；
  2. 当前指针pT为栈顶节点，若pT为叶子节点，或者最近访问的节点preT是pT的左孩子或右孩子，访问当前节点并出栈，最近访问节点preT为当前的节点；否则，将pT的右孩子入栈，再将其左孩子入栈；

后序遍历（非递归）的Java代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void PostOrderTraversalNonRecursive(Node T) {
    List<Node> stack = new ArrayList<>();
    stack.add(T);
    Node pT;
    Node preT = null;
    while(!stack.isEmpty()) {
        pT = stack.get(stack.size() - 1);
        if((pT.left == null && pT.right == null) ||
           (preT != null && (preT == pT.left || preT == pT.right))) {
            System.out.println(pT.value);
            preT = pT;
            stack.remove(stack.size() - 1);
        } else {
            if(pT.right != null) {
                stack.add(pT.right);
            }
            if(pT.left != null) {
                stack.add(pT.left);
            }
        }
    }
}
文章目录
  1. 1. 二叉树定义
  2. 2. 前序遍历
  3. 3. 中序遍历
  4. 4. 后序遍历